2º Ano – Matemática 2 – 22/05/2020

Bom dia pessoal,

A nossa aula de hoje de matemática 2 constará de 3 atividades que deverão ser entregues em uma única mensagem contendo:

O arquivo da atividade 1.

A resposta por escrito da atividade 2.

O arquivo e a resposta por escrito da atividade 3.

ATIVIDADE 1

Estude os tutoriais do GeoGebra 5 de números 23 e 24 disponíveis no seguinte endereço (escolha a opção “VÍDEOS TUTORIAIS” no menu principal):

http://www.geogebra.im-uff.mat.br/

Nestes tutoriais, você aprenderá a usar descrições algébricas e a Janela de Álgebra do GeoGebra 5. Atenção: recomendamos que, além de assistir aos tutoriais, você tente, concomitantemente, reproduzir as instruções apresentadas! Afinal, uma coisa é ver, outra é fazer.
Implemente a construção descrita no tutorial 24 e, então, salve-a com o nome “tutorial-24.ggb”.

ATIVIDADE 2

No GeoGebra 5, construa um círculo C e, em seguida, marque um segmento AB cujas extremidades pertencem a C. Construa então um ponto semilivre P sobre o círculo C, marque e meça o ângulo θ = ∠APB. Construa também a bissetriz deste ângulo.

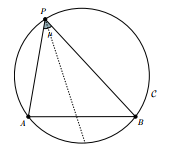
Arraste o ponto P e tente descobrir quais são os invariantes geométricos desta construção, ou seja, ao movimentar o ponto P, o que não irá mudar em nossa figura?

ATIVIDADE 3

Crie no GeoGebra 5 um triãngulo de vértices A, B e C. Renomeie, se necessário, os lados BC, AC e AB do triângulo para a, b e c, respectivamente. Em seguida, construa a altura do triângulo relativa ao lado AC. Renomeie, se necessário, essa altura para h. Defina então, no Campo de Entrada, a seguinte variável algébrica que dá o valor do semiperímetro do
triângulo:

s = (a + b + c)/2

Em seguida, defina as variáveis algébricas

Area1 = (b h)/2 e Area2 = sqrt(s (s – a) (s – b) (s – c))

que dão o valor da área do triângulo (a segunda expressão é conhecida como Fórmula de Heron). Cuidado: é preciso dar um espaço em branco (ou um asterisco) entre “b” e “h” para indicar uma multiplicação entre as variáveis “b” e “h”. Aqui, “sqrt” representa a função raiz quadrada. Importante: mova os pontos A, B e C e certifique-se que sua construção continua válida para quaisquer posições destes pontos. Um questionamento: as áreas 1 e 2 estão com os valores exatamente iguais ou existe uma diferença no arredondamento?

As atividades de hoje serão entregues em uma única mensagem contendo:

• O arquivo da atividade 1.

• A resposta por escrito da atividade 2.

• O arquivo e a resposta por escrito da atividade 3.

Boa sorte e bons estudos!

Mundico